수직다관절로봇 기구학은 보통 DH parameter로 만들어지는 좌표변환 행렬의 연속적인 곱으로 이루어집니다. 기구학을 풀어 로봇의 관절각도로부터 그리퍼의 위치와 방위를 알게됩니다. 그런데 주어진 그리퍼의 위치로부터 관절각도를 계산하는 역기구학을 푸는 것은 쉽지않습니다. 좌표변환 행렬의 요소들은 sin, cos 함수의 조합으로 만들어지는 비선형 함수가 얻어지고 비선형 함수의 역함수를 직접적으로 구할 수 없기때문입니다.
그래서 로봇의 역기구학을 구하려면 대부분 비선형 연립방정식을 수치해석적으로 풀어야합니다. 여기서는 역기구학보다 한단계 더 나아가 로봇의 DH-parameter를 캘리브레이션 하는 방법에 대해 설명해 보겠습니다. DH-parameter를 캘리브레이션 하는 사유로는, 로봇을 설계할 때 설정한 DH parameter 대로 로봇이 만들어지고 원점이 설정되지 않기 때문입니다. 아무리 정교하게 부품을 가공하고 지그를 사용하여 잘 조립했다 하더라도 약간의 오차들이 발생하고 이는 로봇의 그리퍼에서 큰 위치오차를 만들어냅니다.
그런데 실제 산업현장에서 사용되는 로봇들은 캘리브레이션 없이 사용되기도 합니다. 나사를 체결하거나 점용접을 할 때는 각각의 작업 위치들을 작업자가 티칭으로 설정하기때문에 오차를 고려하지 않아도 됩니다. 그런데 캘리브레이션 하지 않은 로봇으로 선을 따라 풀칠을 하거나 용접을 할 때는 로봇의 말단부가 정확한 직선을 따라 그리지 못하게되는 문제가 발생합니다.
이제 비선형 연립 방정식을 어떻게 푸는지 차근차근 알아보겠습니다. 먼저 간단한 다음과 같은 비선형 식 f(x)=0이 있을 때 x 값을 구하는데 Newton-Raphson 법을 사용합니다. 이 풀이법은 인터넷에 그림과 함께 자료가 많기때문에 상세하게 설명하지 않겠습니다.
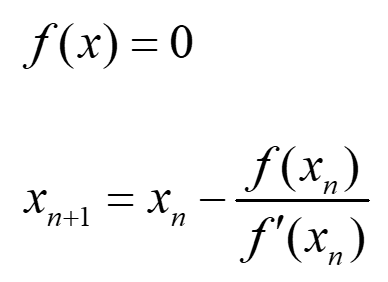
비선형식을 푸는 Newton-Raphson 법은 함수의 Taylor 전개를 통해 구하게됩니다. 그러면 비선형 연립 방정은 어떻게 풀까요? 이것도 함수를 Taylor 전개한 식에서 고차항은 버리고 1차항 까지만 사용하여 구하게 됩니다. 그러면 비선형식의 Newton-Raphson 법과 모양이 같아집니다. 행렬 형태로 바뀌기때문에 좀 헷갈리지만 형태는 같습니다.
다음과 같은 비선형 연립방정식이 있을 때,
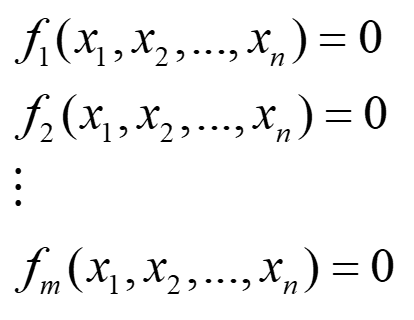
Taylor 전개를 1차항 까지만 하고 f(..) = 0인 관계로 원 함수를 소거하면 다음과 같은 모양이 됩니다.
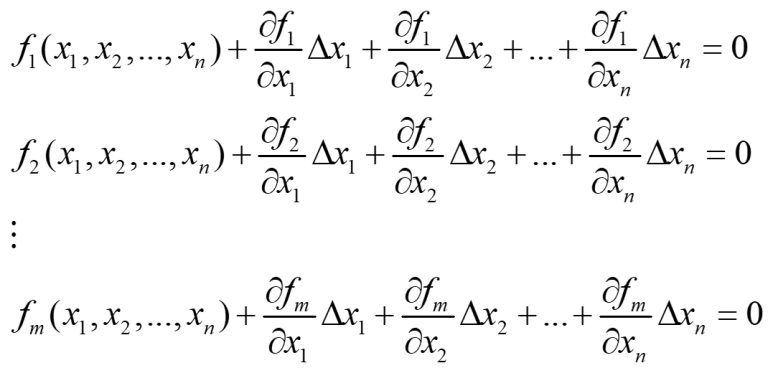
위 식을 행렬 형태로 바꿉니다.
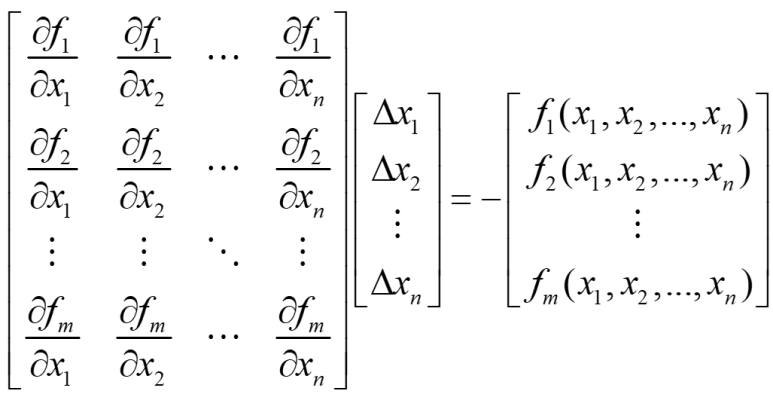
행렬 A가 정방행렬일 때(m==n) 다음과 같이 A의 역행렬을 계산합니다. 그리고 Δx를 반복계산하여 x에 업데이트 해나가다보면 점점 정확한 해를 얻을 수 있습니다.
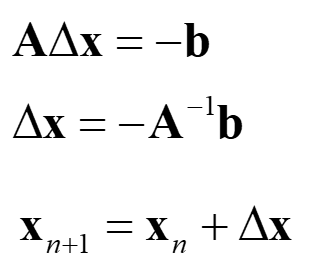
풀이 예제
이해를 돕기위해 간단한 예제를 풀어보겠습니다.
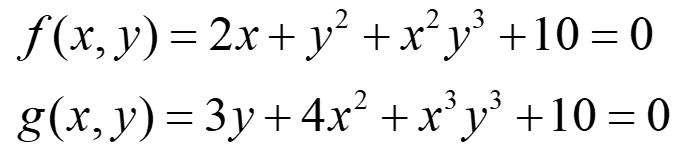
위 식을 Newton-Raphson 법으로 푸는 C 코드를 작성합니다.
// 비선형 연립방정식 풀이 (non-linear equation)
// Newton-Raphson method로 푼다
// f(x,y) = 2*x + y^2 + x^2*y^3 + 10 = 0
// g(x,y) = 3*y + 4*x^2 + x^3*y^3 + 10 = 0
double ff (double x, double y) { return 2*x + y*y + x*x*y*y*y + 10; }
double fg (double x, double y) { return 3*y + 4*x*x + x*x*x*y*y*y + 10; }
double dfx(double x, double y) { return 2 + 2*x*y*y*y; }
double dfy(double x, double y) { return 2*y + 3*x*x*y*y; }
double dgx(double x, double y) { return 8*x + 3*x*x*y*y; }
double dgy(double x, double y) { return 3 + 3*x*x*x*y*y; }
#define MAT_EPS (1e-30f)
inline bool InvMat2 (double x[2][2], double A[2][2])
{
double den = A[0][0]*A[1][1] - A[0][1]*A[1][0];
if (-MAT_EPS < den && den < MAT_EPS) return false;
x[0][0] = A[1][1]/den; x[0][1] = -A[0][1]/den;
x[1][0] = -A[1][0]/den; x[1][1] = A[0][0]/den;
return true;
}
inline void MulMatVec2 (double x[2], double A[2][2], double v[2])
{
x[0] = A[0][0]*v[0] + A[0][1]*v[1];
x[1] = A[1][0]*v[0] + A[1][1]*v[1];
}
int _tmain(int argc, _TCHAR* argv[])
{
double d[2];
double o[2];
double J[2][2];
double Ji[2][2];
// 찾고자 하는 해의 초기치 설정
double x = 0;
double y = 0;
for (int i=0; i<300; i++) {
o[0] = -ff(x,y);
o[1] = -fg(x,y);
// Jacobian
J[0][0] = dfx(x,y); J[0][1] = dfy(x,y);
J[1][0] = dgx(x,y); J[1][1] = dgy(x,y);
InvMat2(Ji, J);
MulMatVec2(d, Ji, o);
x += d[0];
y += d[1];
if (i%10 == 0) {
printf ("[%d] x = %f, y = %f --> ", i, x, y);
printf ("f error = %f, g error = %f \n", ff(x,y), fg(x,y));
}
}
return 0;
}소스코드를 컴파일하고 링크하여 실행합니다.
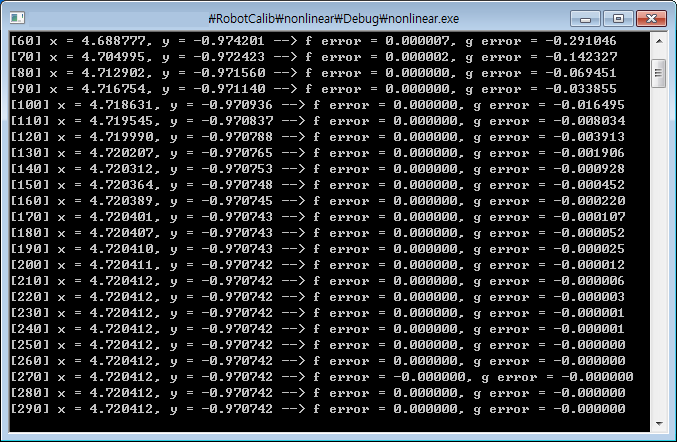
290회 정도 반복 계산하면 에러가 모두 0으로 수렴하며, 소숫점 6 자리까지 정밀도로 답을 구할 수 있습니다.
'로봇' 카테고리의 다른 글
| Base, Tool offset이 있을 때의 SCARA 로봇 기구학 파라미터 오차 보정 (0) | 2023.10.08 |
|---|---|
| SCARA 로봇의 기구학 파라메터 오차 보정(Levenberg–Marquardt method) (1) | 2023.10.08 |
| 로봇 조인트의 영점 보정(Gauss-Newton method) (0) | 2023.10.08 |
| 바이오 메디컬 로봇 소개 (0) | 2023.10.08 |
| 고속 Pick and place 용 델타봇 제작 (0) | 2023.10.08 |



