이전 글(https://blog.naver.com/pg365/223228331354)에서 간단한 비선형 연립방정식을 Newton-Raphson 방법으로 풀어보았습니다. 이번에는 n개의 조인트 (θ1~θn)를 가지는 로봇의 기구학식 f1~fm에 의해 공간상의 위치와 방위 (p1~pm)를 계산할 수 있는 가상의 로봇을 가정해 보겠습니다. 로봇의 기구학 식을 다음과 같이 표기하겠습니다.
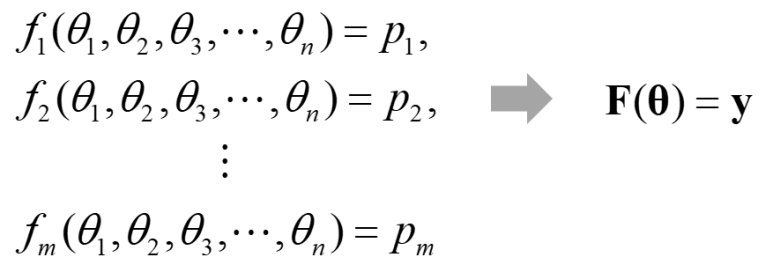
우리는 이 가상의 로봇에서 조인트 홈잉 완료 후 0점이 얼마나 틀어져 있는지를 알고싶은 상황입니다. 그래서 로봇의 조인트 각도를 입력하여 로봇을 움직인 후 정밀한 센서를 사용하여 로봇 말단의 위치 y를 모두 측정해둔 상황입니다.
위 식에서 Joint의 영점 오차(ε1~εn)가 포함되어 있다면 다시 다음과 같이 적을 수 있습니다. 위에서 말했듯이 조인트의 각도와 말단의 위치는 이미 알고있기때문에 함수 F(θ) 를 F(θ,x)로 바꾸겠습니다(x는 조인트 영점 오차에 대한 벡터). 왜냐하면 우리가 알고싶은것은 조인트의 영점 오차이기때문입니다.
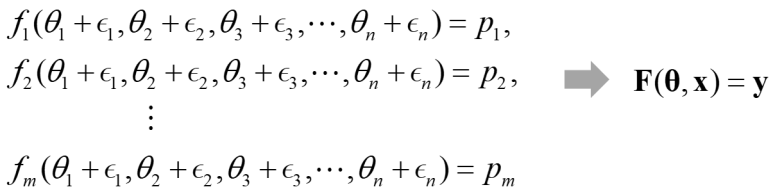
식이 완성되었으니 이제 이전 글에서와 같이 Newton-Raphson 법으로 조인트의 오차를 구하면 됩니다. 이전 글에서 벡터에 대한 편미분 식들을 행렬 A로 표기하였는데, 이 행렬을 보통 Jacobian matrix라고 부르고 J로 표기합니다. Jacobian matrix는 일차 직선 y=mx 에서 기울기 m과 같습니다. 그런데 로봇의 기구학 식이 비선형이다보니 특정 위치의 아주 좁은 구간에서 선형으로 근사시키고 기울기를 구했다고 보면 됩니다.
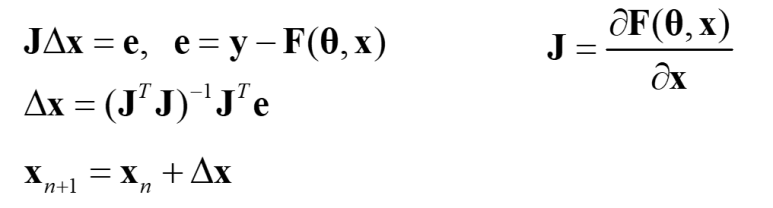
여기서 벡터 e는 센서로 측정한 로봇 말단의 위치값 y와 로봇의 조인트가 θ+ε 각도일 때 기구학식 F로 계산한 값 간의 차이값입니다. 차이값 e가 0이 될 때까지 계속 x를 1/m 만큼 업데이트 해나가다보면 x는 특정 값에 수렴하게 되고 이 값이 우리가 구하고자 하는 조인트 오차 (ε1~εn) 가 됩니다 (m은 J 행렬).
그리고 Newton-Raphson 법을 위와 같이 행렬 형태로 확장한 것을 Gauss-Newton method라고 부릅니다. 위 식에서 m!=n 인경우 정방행렬이 아니기때문에 역행렬을 바로 계산할 수 없습니다. 이런 경우 의사역행렬을 계산하는데, Moore-Penrose inverse 라고도 부르며 자세한 내용은 위키피디아를 참고하면 됩니다: https://en.wikipedia.org/wiki/Moore%E2%80%93Penrose_inverse.
'로봇' 카테고리의 다른 글
| Base, Tool offset이 있을 때의 SCARA 로봇 기구학 파라미터 오차 보정 (0) | 2023.10.08 |
|---|---|
| SCARA 로봇의 기구학 파라메터 오차 보정(Levenberg–Marquardt method) (1) | 2023.10.08 |
| 비선형 연립 방정식 풀이 (Newton-Raphson method) (0) | 2023.10.08 |
| 바이오 메디컬 로봇 소개 (0) | 2023.10.08 |
| 고속 Pick and place 용 델타봇 제작 (0) | 2023.10.08 |



