SCARA (Selective Compliance Assembly Robot Arm) 로봇의 기구학부터 알아보겠습니다. 스카라 로봇은 평면상에서 두 개의 조인트와 링크가 움직입니다. 그래서 순기구학과 역기구학을 간단하게 계산할 수 있습니다.
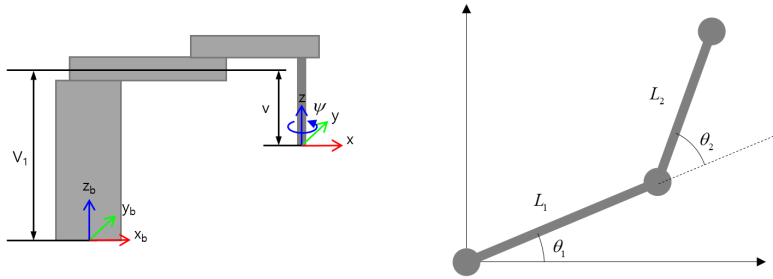
순기구학과 역기구학 식은 아래와 같습니다. 다음 과정에서는 순기구학 식만 사용되니 역기구학은 참고로만 봐주십시오.

이전 글 "로봇 조인트의 영점 보정"(https://blog.naver.com/pg365/223230236951) 에서 Gauss-Newton method로 영점 보정하는 방법을 알아보았습니다. 이번에는 약간 업그레이드 된 Levenberg-Marquardt method로 SCARA 로봇의 기구학 파라메터 오차 보정 방법을 알아보겠습니다. Levenberg-Marquardt 법은 Damped least-squares(DLS) 라고도 합니다. DLS는 로봇 역기구학을 계산할 때 특이점(singularity) 부근에서 댐핑을 주어 특이점을 회피하도록 합니다.
SCARA 로봇을 설계할 때는 아래 왼쪽과 같이 이상적인 모델 파라미터를 가지고 있을것입니다. 그런데 조인트와 링크를 가공하여 조립하였더니 오른쪽과 같은 실제 모델 파라미터를 가졌다고 고려합시다. 아직 우리는 실제 모델 파라미터를 모릅니다. 지금 우리가 아는 것은 이상적인 모델 파라미터만 알고있습니다.

이제 실제 만들어진 로봇에다가 5개의 각각 다른 관절 변위를 설정하여 로봇의 말단이 위치하는 곳을 측정해봅니다. 가상의 로봇이기때문에 측정할수는 없고 기구학 식에 실제 모델 파라메터로 계산하는 과정이겠죠. 결과적으로 다음과 같이 다섯개의 말단 위치 y1~y5를 얻게 됩니다.

그런데 지금 우리는 로봇의 이상적인 모델에 대한 파라미터만 알고있습니다. 그래서 실험에 사용한 데이터(관절 변위와 로봇 말단위치)를 이상적인 모델에 대한 기구학 F(x)에 적용하여 실제 측정값 y와의 오차 e를 계산할 수 있습니다.
이전 글에서 Newton-Raphson 법으로 조인트 오차를 계산할 때와 같은 형태의 식으로 만듭니다.
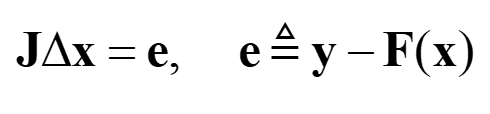
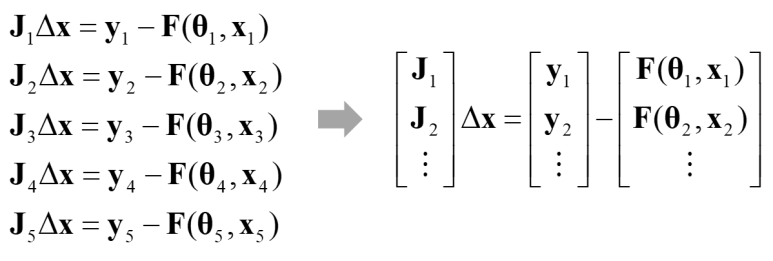
여기서 x, f, F(x), J는 다음과 같습니다.


식을 만들었습니다. 이제 오차 e가 0이 될 때까지 Levenberg-Marquardt 법으로 반복계산하면 x가 실제 모델에 대한 파라미터 값으로 수렴하게 됩니다.
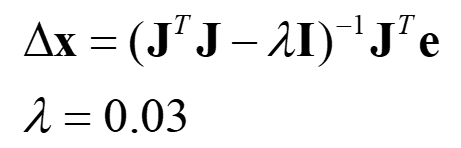
이전 방법과 약간 다른 점이 λI가 추가된것입니다. 이 값이 특이점 근처에서 댐핑 효과를 주어 특이점 근처에서도 inverse를 계산할 수 있게 합니다. λ가 크면 특이점 근처에서 천천히 움직이게 되고 λ가 작으면 빠르게 움직입니다. 실험으로 적당한 값을 선택하면 됩니다.

그리고 x를 업데이트 할 때 1보다 작은 α값을 주어 x가 발산하지 않도록 합니다. 당연히 1일 때보다 수렴 속도는 느려지지만 안정적으로 해에 수렴하게 됩니다.
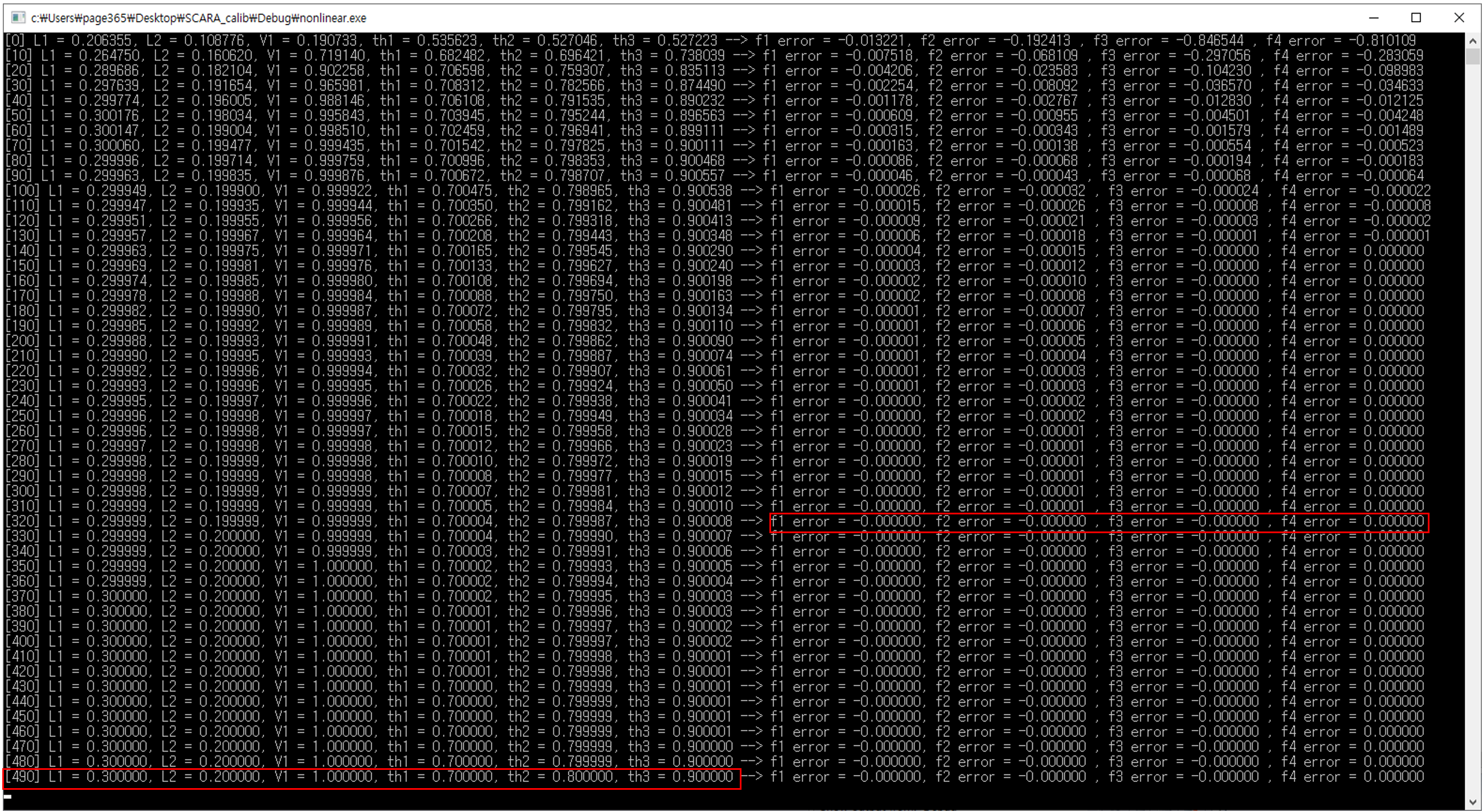
300회 정도 반복 계산하면 소숫점 6 자리까지(μm) 정밀도로 답을 구할 수 있습니다.
'로봇' 카테고리의 다른 글
| Base, Tool offset이 있을 때의 SCARA 로봇 기구학 파라미터 오차 보정 (0) | 2023.10.08 |
|---|---|
| 로봇 조인트의 영점 보정(Gauss-Newton method) (0) | 2023.10.08 |
| 비선형 연립 방정식 풀이 (Newton-Raphson method) (0) | 2023.10.08 |
| 바이오 메디컬 로봇 소개 (0) | 2023.10.08 |
| 고속 Pick and place 용 델타봇 제작 (0) | 2023.10.08 |



